Computação em paralelo no R: Conceitos básicos
Introduction
Neste tutorial trabalharemos aspectos básicos de programação em paralelo utilizando o software R. Para isso, serão necessários os pacotes doParallel e foreach para programação utilizando os processadores da máquina, e para a programação utilizando uma placa gráfica (GPU) traremos alguns aspectos introdutórios.
Parallel computation
O assunto computação paralela data de 1958 quando John Cocke e Daniel Slotnick discutiram o uso do paralelismo para cálculos numéricos pela primeira vez na IBM.
Segundo a Wikipedia Computação paralela é uma forma de computação em que vários cálculos são realizados ao mesmo tempo, operando sob o princípio de que grande problemas geralmente podem ser divididos em problemas menores, que então são resolvidos concorrentemente (em paralelo).
Naturalmente paralelizamos processos no nosso dia-a-dia. Por exemplo, quando trabalhamos em uma empresa, divide-se o problema em pequenas partes em que cada parte é executada por um grupo de forma paralela. Dentro deste grupo ainda é possível subdividir a parte do problema em subtarefas que também podem ser executadas de forma paralela.
Desta forma, computação em paralelo foge do pensamento sequencial (quando possível). Por exemplo, para calcular a média de idade de cada curso de graduação da UFMG, não é necessário que os cálculos sejam realizados de forma sequencial, pois, a média de idade de um curso não influencia na média de idade de um outro curso e portanto neste caso podemos paralelizar o cálculo. Já quando estamos trabalhando com um problema iterativo em que o valor corrente depende do valor imediatamente anterior não é possível paralelizar a computação (Ex: Gibbs Sampling).
A computação em paralelo depende de quantos processadores você dispoem, de forma que quanto maior o número de processadores maior a capacidade de executar processos simultaneamente. Existem duas leis que mensuram o aumento de velocidade de computação utilizando programação em paralelo.
A lei de Amdahl é dada por \(\displaystyle S = \frac{1}{1-P+\frac{P}{S_P}}\), em que S é a aceleração na execução do processo com a paralelização, \(P\) é a fração paralelizável do código e \(S_P\) é o tempo de execução da parte paralelizável (com a melhoria). Por exemplo, se 30% do código é paralelizável e com a melhoria esta parte o código é executada duas vezes mais rápido, então o aumento de velocidade de computação é dado por \(\displaystyle S = \frac{1}{1-0.3+\frac{0.3}{2}} = 1.18\). Ou seja um código que é executado em 590 segundos sem paralelização, teria o tempo de computação reduzido para 500 segundos.
Outra forma de estimar a aceleração na execução do processo é dada pela lei de Gustafson definida por \(S = 1-P+P*S_P\). Abaixo um gráfico contrapondo as duas curvas em um caso específico.
library(ggplot2)
library(plotly)
library(ggthemes)
library(foreach)
library(doParallel)
#--- Parâmetros gráficos
colAxis <- grey(0.4)
colTitle <- grey(0.2)
colPoints <- "#0b5394"
colLine <- "IndianRed"
colGroup1 <- "#1F77B4"
colGroup2 <- "#D62728"
colBack <- "white"
sizePoint <- 2
sizeLine <- 1.3
tema <- theme_stata() +
theme(axis.title = element_text(size = 12, margin = margin(10,10,0,0)),
axis.text = element_text(size = 12, colour = colAxis),
panel.background = element_rect(fill = colBack),
plot.background = element_rect(fill = colBack))
#--- Leis de A mdahl e Gustafson
s_1 <- function(p, s) 1/(1-p+p/s)
s_2 <- function(p, s) 1-p+p*s
seq_proc <- seq(1, 15)
p_1 <- 0.70
p_2 <- 0.30
df_proc <- data.frame(
n_proc = rep(seq_proc, 4),
S = c(
s_1(p = p_1, s = seq_proc),
s_1(p = p_2, s = seq_proc),
s_2(p = p_1, s = seq_proc),
s_2(p = p_2, s = seq_proc)
),
p = paste0("P = ", rep(c(p_1, p_2), 2, each = length(seq_proc))),
Tipo = rep(c(rep("Amdahl", length(seq_proc)), rep("Gustafson", length(seq_proc))), each = 2)
)
gg_proc <- ggplot(data = df_proc, aes(x = n_proc, y = S, colour = Tipo)) +
geom_line(size = sizeLine) +
scale_color_manual("", values = c("Amdahl" = "Steelblue",
"Gustafson" = "IndianRed")) +
xlab("Número de processadores") +
ylab("Aceleração de processamento") +
tema +
theme(legend.position = "top") +
facet_wrap(~p)
gg_proc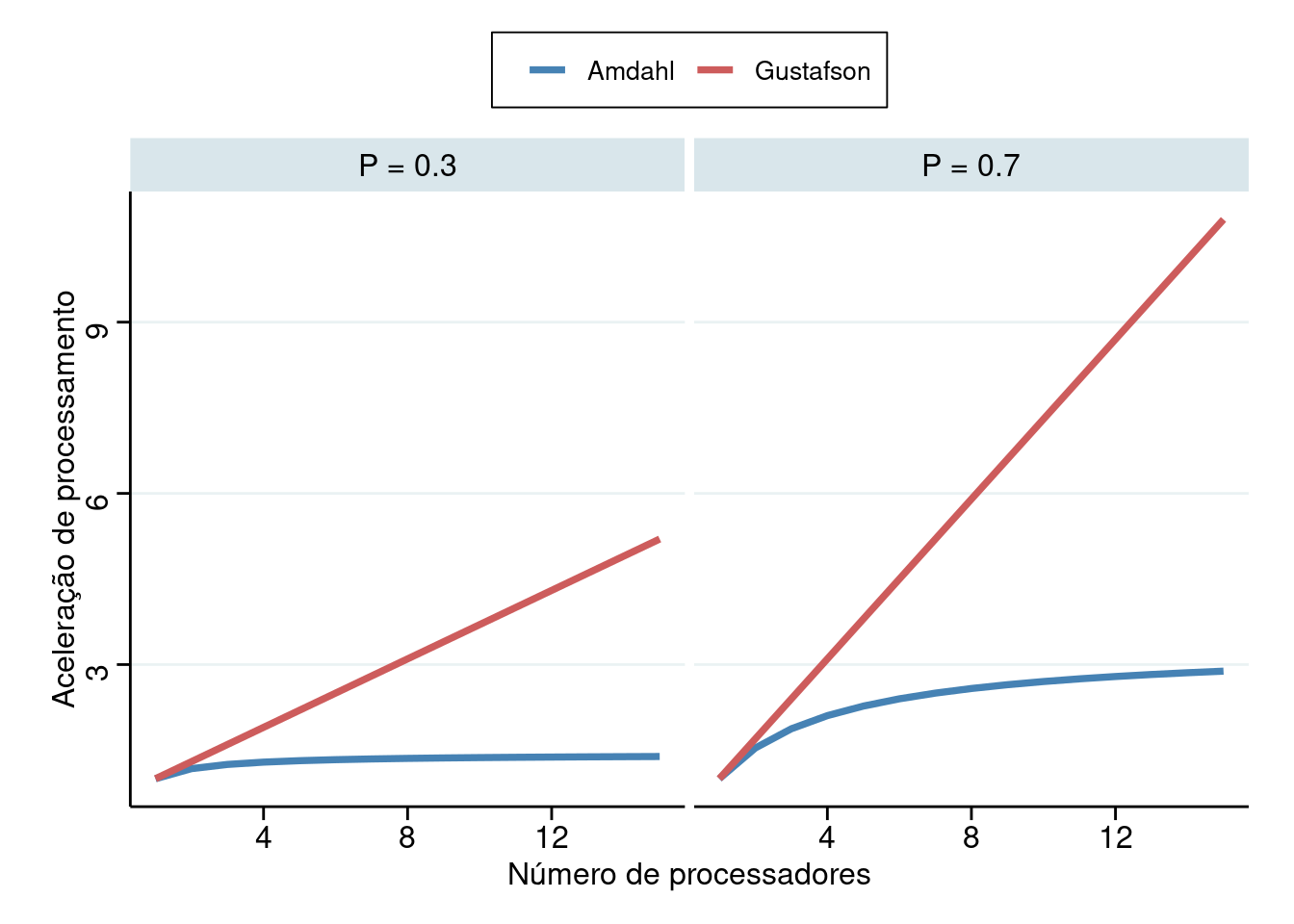
Nota-se que a lei de Gustafson é menos pessimista que a lei de Amdahl quanto ao aumento de velocidade de processamento. De fato, a lei de Gustafson indica que a aceleração de processamento é linear no número de processadores enquanto que a lei de Amdahl é mais conservadora e tende a ser constante \(\left(S = \frac{1}{1-p}\right)\) quando o número de processadores cresce.
Com estas leis é possível ter uma estimativa da melhora de performance de um código ao se utilizar computação paralela.
Porém, as vezes o custo computacional de se paralelizar o código pode ser maior que o ganho na velocidade de execução. Isso faz com que o custo computacional paralelizando o código seja maior do que o custo computacional sequencial. Este problema é conhecido como lentidão paralela.
Para exemplificar o fenômeno da lentidão paralela pense no seguinte exemplo: Você é um garçom em uma festa e tem trezentas taças para servir. Obviamente você não irá servir de uma em uma, então, com auxílio de uma bandeja você pode paralelizar o processo levando algumas taças. Porém, vai existir um número de taças na bandeja o qual o acrescimo de mais uma taça faz com que o processo de equilibrar a bandeja e servir mais complicado podendo inclusive provocar a queda da bandeja. Nesse caso a paralelização acaba sendo um problema e não uma solução.

Motivação
Agora que já sabemos o que é computação paralela vamos à um exemplo prático. Vamos executar de tres formas diferentes o mesmo codigo. O comando for fará o loop usual (sequencial). O comando foreach em conjunto com o operador %do% também fará o loop sequencial. Já o comando foreach em conjunto com o operador %dopar% fará o loop em paralelo.
Para comparar os tempos de execução vamos utilizar a função benchmark do pacote rbenchmark.
library(rbenchmark)
library(foreach)
library(doParallel)
registerDoParallel(cores = detectCores())
sleep_time <- 0.1
bench <- benchmark(
"for" = for(i in 1:4){Sys.sleep(sleep_time)}, # Sequencial
"do" = foreach(n = 1:4) %do% Sys.sleep(sleep_time), # Sequencial
"dopar" = foreach(n = 1:4) %dopar% Sys.sleep(sleep_time), # Paralelizado
columns = c("test", "replications", "elapsed", "user.self", "sys.self")
)
bench <- bench[order(bench$elapsed),]
bench[, 1:3]## test replications elapsed
## 3 dopar 100 14.285
## 1 for 100 40.619
## 2 do 100 40.938Percebe-se que o custo computacional utilizando a função foreach paralelizada é muito menor que o custo associado ao loop sequencial. A função paralelizada tem um tempo de processamento de aproximadamente 14.285 segundos enquanto as demais tem tempos de execução de 40.619 e 40.938 (para realizar 100 replicações de um loop de 4 iterações).
Este é um exemplo simples em que cada passo da iteração tem um tempo computacional de aproximadamente 0.1 segundos. O resultado pode ser muito mais interessante quando pensarmos em um problema em que a função a ser executada dentro do loop tem um tempo computacional mais elevado.
Tipos de paralelismo
Existem várias formas de computação em paralelo. Neste documento vamos falar de dois tipos:
- Paralelismo utilizando os processadores de uma máquina.
- Paralelismo utilizando uma placa gráfica (GPU).
Paralelismo utilizando os processadores de uma máquina
A ideia básica é realizar processos simultâneamente e não sequencialmente. Para isso o procedimento a ser executado deve ser paralelizável e a máquina deve possuir mais do que um processador (o que é natural hoje em dia).
Para descobrir o número de processadores da sua máquina basta utilizar a função detectCores do pacote parallel,
parallel::detectCores()## [1] 12Desta forma, é possível realizar em paralelo 12 processos nesta máquina. Para ilustrar a paralelização vamos utilizar o pacote do R foreach.
foreach
O pacote foreach possui uma forma diferente de executar códigos repetidamente no R. O principal diferencial do pacote é ter a opção de se realizar o loop em paralelo usando os processadores da sua máquina. Desta forma, operações que levam minutos utilizando a abordagem sequencial podem ser reduzidas à segundos de computação.
Primeiramente é interessante observar a forma como o pacote realiza o loop sequencial. Para isso utiliza-se o operador %do%, veja o exemplo abaixo:
raiz <- foreach(i=1:3) %do% sqrt(i)
raiz## [[1]]
## [1] 1
##
## [[2]]
## [1] 1.414214
##
## [[3]]
## [1] 1.732051Perceba que por default a saída é uma lista, diferente do loop convencional (for) que retorna um vetor. De fato, o parâmetro .combine retorna o resultado do loop da maneira que o usuário achar mais adequado. Essa funcionalidade pode ser muito útil dependendo da aplicação.
raiz_c <- foreach(i=1:3, .combine = 'c') %do% sqrt(i)
raiz_c## [1] 1.000000 1.414214 1.732051raiz_rbind <- foreach(i=1:3, .combine = 'rbind') %do% sqrt(i)
raiz_rbind## [,1]
## result.1 1.000000
## result.2 1.414214
## result.3 1.732051Para realizar o loop em paralelo utiliza-se o operador dopar. Além disso, é necessário criar um registro de quantos processadores serão utilizados no processamento. Esse registro pode ser feito utilizando o pacote doParallel.
registerDoParallel(detectCores())
n <- 10
unif <- runif(n = n)
system.time(
foreach(i = 1:n, .combine = 'c') %do% {
Sys.sleep(unif)
i
}
)## user system elapsed
## 0.005 0.000 0.584system.time(
foreach(i = 1:n, .combine = 'c') %dopar% {
Sys.sleep(unif)
i
}
)## user system elapsed
## 0.016 0.058 0.086Com esse simples exemplo pode-se observar a grande diferença no tempo de execução entre o loop sequencial e o loop paralelizado.
Para mostrar a potencialidade da função vamos criar alguns exemplos. É interessante observarmos a diferença de tempo quando estamos trabalhando com algum processo custoso computacionalmente.
Normalmente em artigos, teses e dissertações em Estatística utilizam-se simulações extensivamente. Nestas simulações por muitas vezes variam-se alguns parâmetros do modelo e avaliam-se os resultados para cada configuração. Esse processo é chamado de análise de sensibilidade.
Neste sentido, vamos supor que temos acesso à \(n\) covariáveis e vamos implementar um modelo de regressão linear para cada combinação possível dessas \(n\) covariáveis (modelo guloso de seleção de covariáveis).
library(mvtnorm)
nCov <- n
n <- 100000
seq_n <- 1:nCov
cov <- data.frame(rmvnorm(n = n, mean = rep(0, nCov)))
data <- cov
data$y <- rnorm(n)
comb <- Map(combn, list(seq_n), seq_along(seq_n), simplify = FALSE)
vars <- unlist(comb, recursive = FALSE)
t1 <- system.time(
res_do <- foreach(i = 1:(2^nCov - 1), .combine = 'rbind') %do% {
formula <- paste("y ~ ", paste0("X", vars[[i]], collapse = " + "))
reg <- lm(formula = formula, data = data)
df <- data.frame(i = i, AIC = AIC(reg))
df
}
)
t1[3]
t2 <- system.time(
res_dopar <- foreach(i = 1:(2^nCov - 1), .combine = 'rbind') %dopar% {
formula <- paste("y ~ ", paste0("X", vars[[i]], collapse = " + "))
reg <- lm(formula = formula, data = data)
df <- data.frame(i = i, AIC = AIC(reg))
df
}
)
t2[3]## elapsed
## 200.713## elapsed
## 57.297Pode-se ver que o tempo de processamento do loop em paralelo é muito menor do que o loop sequencial. O tempo computacional do código paralelizado é igual a 28.55% do tempo computacional do código sequencial.
Neste caso 100% do código é paralelizável e desta forma as leis de Amdhal e Gustafson possuem a mesma estimativa de aceleração no tempo de execução. As estimativas de aceleração de ambas as leis é 4, desta forma espera-se que de fato, o código paralelizado seja 4 vezes mais rápido.
Outro contexto em que a paralelização pode ser útil é quando temos um modelo de aprendizado de máquina com diversos parâmetros de tunagem. Em geral testa-se algumas configurações destes parâmetros e escolhe-se o modelo que minimiza alguma função objetivo. Para ilustrar esse caso vamos utilizar o modelo SVM para classificação.
Para ajustar um modelo de SVM no R vamos utilizar a função svm do pacote e1071. Os hiperparâmetros que serão variados serão: scale, kernel, degree, gamma e cost. Para melhor entendimento dos parâmetros veja ?e1071::svm.
library(e1071)
#--- Criando uma base de dados
nCov <- 10
n <- 5000
X <- rmvnorm(n = n, mean = rep(0, nCov))
betas <- rnorm(n = nCov)
Xbeta <- X%*%betas
y <- ifelse(Xbeta < 0.5, 0, 1)
data <- data.frame(y = y, X)
#--- Separando a base em treino e teste
id <- 1:nrow(data)
testindex <- sample(id, trunc(length(id)/3))
testset <- data[testindex,]
trainset <- data[-testindex,]
#--- Criando os grids para avaliação dos parâmetros de tunagem
scale = c(TRUE, FALSE)
kernel = c("linear", "polynomial", "radial", "sigmoid")
degree = 2:4
gamma = 1/seq(nrow(trainset)-(n/10), nrow(trainset) + (n/10), length.out = 4)
cost = seq(1, 10, length.out = 4)
parameters <- expand.grid(scale = scale,
kernel = kernel,
degree = degree,
gamma = gamma,
cost = cost)
#--- SVM sem paralelização
t1 <- system.time(
svm.output_1 <- foreach(i = 1:nrow(parameters), .combine = 'rbind') %do% {
#--- Modelo
svm.model <- svm(formula = y ~ .,
data = trainset,
scale = parameters[i, 1],
kernel = parameters[i, 2],
degree = parameters[i, 3],
gamma = parameters[i, 4],
cost = parameters[i, 5],
type = "C-classification")
#--- Predição
svm.pred <- predict(svm.model, testset[,-1])
#--- Métrica de acurácia
svm.confusao <- table(pred = svm.pred, true = testset[,1])
svm.acuracia <- sum(diag(svm.confusao))/sum(svm.confusao)
#--- Retornando os resultados
cbind(parameters[i,], acuracia = svm.acuracia)
}
)
#--- SVM com paralelização
t2 <- system.time(
svm.output_2 <- foreach(i = 1:nrow(parameters), .combine = 'rbind') %dopar% {
#--- Modelo
svm.model <- svm(formula = y ~ .,
data = trainset,
scale = parameters[i, 1],
kernel = parameters[i, 2],
degree = parameters[i, 3],
gamma = parameters[i, 4],
cost = parameters[i, 5],
type = "C-classification")
#--- Predição
svm.pred <- predict(svm.model, testset[,-1])
#--- Métrica de acurácia
svm.confusao <- table(pred = svm.pred, true = testset[,1])
svm.acuracia <- sum(diag(svm.confusao))/sum(svm.confusao)
#--- Retornando os resultados
cbind(parameters[i,], acuracia = svm.acuracia)
}
)
t1[3]
t2[3]
all.equal(svm.output_1, svm.output_2)
best.config <- svm.output_2[which.max(svm.output_2$acuracia), ]
best.config## elapsed
## 231.401## elapsed
## 101.834## [1] TRUE## scale kernel degree gamma cost acuracia
## 1 TRUE linear 2 0.0003528582 1 0.9957983Neste problema vemos que o código com a paralelização teve um tempo computacional equivalente a 44.01% do tempo computacional da versão não paralelizada. O que neste contexto reflete em um ganho de 2.1594 minutos no tempo de processamento.
Pensando nas leis de Amdahl e Gustafson (ambas resultariam em uma aceleração de 4 vezes para este caso em que o código é 100% paralelizável) a estimativa para a aceleração no tempo de execução do código é acertiva.
Abaixo temos duas figuras, uma mostrando o uso dos processadores enquanto o loop sequencial rodava e outra enquanto o loop paralelizado rodava. É possível perceber que de fato o loop sequencial utiliza apenas um processador enquanto o loop paralelizado utiliza todo o potencial computacional.
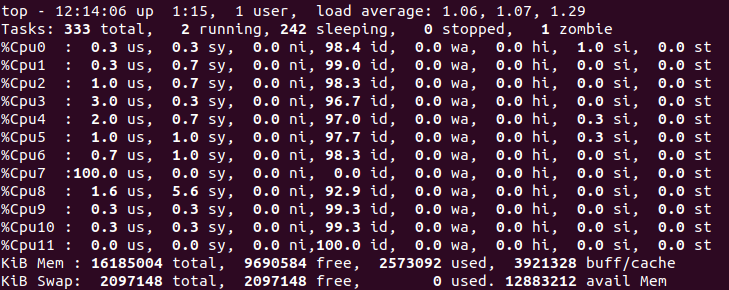
Processadores durante o loop não paralelizado
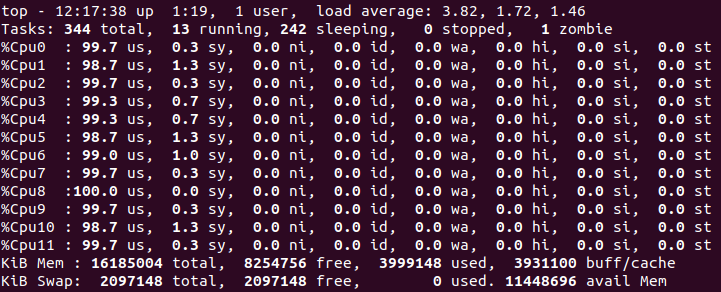
Processadores durante o loop paralelizado
Com isso, é interessante ressaltar que quanto maior o número de processadores maior o ganho ao se paralelizar um código.
Uma ideia interessante é investigar o que ocorre quando declararamos mais processadores do que o próprio número de processadores da máquina. Isto pode fazer sentido quando o processo a ser executado consome pouco processamento. Obviamente, declarando muito mais processadores do que o número existente podemos cair num problema de lentidão paralela (exemplo do garçom). No exemplo abaixo temos a comparação dos tempos de execução considerando diferentes números de processadores (lembrando que a minha máquina possui 12 processadores).
function_test <- function(
cores,
X = rmvnorm(n = 2000, mean = rep(0, 50)),
sleep.time = 0.0001, n
) {
#--- Registrando o número de processadores
registerDoParallel(cores)
#--- Loop
foreach(i = 1:n, .combine = 'c') %dopar% {
#--- Custo de processamento
result <- X%*%t(X)
#--- Custo de tempo
Sys.sleep(sleep.time)
}
}
X = rmvnorm(n = 150, mean = rep(0, 150))
sleep.time <- 1.5*system.time(X%*%t(X))
n <- 100
t001 <- system.time(function_test(cores = 1, X = X, sleep.time = sleep.time, n = n))[3]
t002 <- system.time(function_test(cores = 2, X = X, sleep.time = sleep.time, n = n))[3]
t004 <- system.time(function_test(cores = 4, X = X, sleep.time = sleep.time, n = n))[3]
t008 <- system.time(function_test(cores = 8, X = X, sleep.time = sleep.time, n = n))[3]
t012 <- system.time(function_test(cores = 12, X = X, sleep.time = sleep.time, n = n))[3]
t016 <- system.time(function_test(cores = 16, X = X, sleep.time = sleep.time, n = n))[3]
t025 <- system.time(function_test(cores = 25, X = X, sleep.time = sleep.time, n = n))[3]
t032 <- system.time(function_test(cores = 32, X = X, sleep.time = sleep.time, n = n))[3]
t050 <- system.time(function_test(cores = 50, X = X, sleep.time = sleep.time, n = n))[3]
t064 <- system.time(function_test(cores = 64, X = X, sleep.time = sleep.time, n = n))[3]
t075 <- system.time(function_test(cores = 75, X = X, sleep.time = sleep.time, n = n))[3]
t090 <- system.time(function_test(cores = 90, X = X, sleep.time = sleep.time, n = n))[3]
t100 <- system.time(function_test(cores = 100, X = X, sleep.time = sleep.time, n = n))[3]
tempos <- data.frame(tempos = c(t001, t002, t004,
t008, t012, t016,
t025, t032, t050,
t064, t075, t090,
t100),
processadores = c(1, 2, 4, 8,
12, 16, 25,
32, 50, 64,
75, 90, 100))
tempos## tempos processadores
## 1 1.118 1
## 2 0.507 2
## 3 0.228 4
## 4 0.129 8
## 5 0.117 12
## 6 0.127 16
## 7 0.193 25
## 8 0.213 32
## 9 0.294 50
## 10 0.360 64
## 11 0.411 75
## 12 0.485 90
## 13 0.540 100Não utilizei a função benchmark para garantir que em nenhum momento houvessem processos concorrentes. Vejamos graficamente o que ocorreu nesta simulação:
ggTime <- ggplot(data = tempos, aes(x = processadores, y = tempos)) +
geom_line(col = colLine, size = sizeLine) +
geom_point(col = colPoints, size = sizePoint) +
xlab("Número de processadores") +
ylab("Tempo de processamento") +
tema
ggplotly(ggTime)É possível ver que o tempo de execução tende a decrescer até o momento em que consideramos 12 processadores. Depois deste ponto o tempo computacional começa a crescer (inclusive podendo ser menos vantajoso que o loop sequencial). Obviamente o interessante seria realizar um processo similar ao realizado pelo benchmark, ou seja, executar algumas vezes o mesmo processo e em seguida observar alguma medida de tendência central para melhor representar o custo computacional do processo.
Diversos outros pacotes do R se propõe a realizar a paralelização tal como o pacote snow e o pacote parallel. Porém, o pacote foreach parece atender bem às expectativas além de ser muito simples e intuitivo.
Atualmente o tipo de paralelismo mais utilizado e com melhores resultados é o paralelismo utilizando placas gráficas (GPU) que vamos discutir a seguir.
Paralelismo utilizando uma placa gráfica
Em sua origem na década de 70, a placa gráfica (ou placa de vídeo) era um componente utilizado simplesmente para aumentar a velocidade de apresentação de imagens em jogos arcade.

Depois de vários avanços, as placas de vídeo passaram a ser utilizadas em outros contextos, especialmente em Machine Learning. Desde então os fabricantes de placas gráficas não se preocupam só em criar placas voltadas para games ou softwares 3D e sim placas especiais (e caras) utilizadas para aprendizado de máquina. Mas porquê?
Um vídeo bastante motivador que tenta explicar as diferenças entre processamento utilizando os cores do computador e o processamento utilizando uma placa gráfica pode ser visto abaixo.
Apesar do exagero, a programação utilizando Graphics Processing Unit (GPU) pode ser extremamente mais eficiente do que a programação utilizando os processadores da máquina. Isso pois um computador possui um número limitado de processadores (grandes) pensados e otimizados para processamentos sequenciais. Já uma GPU é idelizada justamente para realizar processos em paralelo, desta forma são milhares de pequenos processadores otimizados para computação paralela (este tipo de computação também é chamada de General Purpose Graphics Processing Unit - GPGPU).
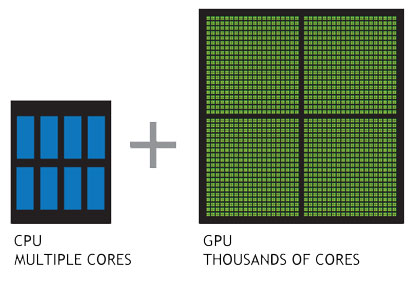
Como nem tudo são flores, a programação utilizando GPU tem a sua limitação. A maioria das placas existentes não possui muita memória o que implica em processamento de pequenas quantidades de dados. Desta forma o processo deve ser raduzido à pequenas subtarefas que não exijam muita memória.
Um simples exemplo de processo paralelizável em GPU é o produto matricial. Na verdade o produto matricial pode ser pensado como produto independente de linhas e colunas. Cada entrada da matriz resposta é na verdade o produto de uma linha por uma coluna, termo a termo, somados. Desta forma, o produto de uma matriz de 1000 linhas e 1000 colunas por outra matriz de mesma dimensão pode ser pensada como 1000*1000 processos independentes. Em cada um dos processos temos apenas dois vetores de dimensão 1000 multiplicados e em seguida somados.
Ou seja, o problema pode ser resolvido de forma mais eficiente. Resolvendo esse problema de forma sequencial teríamos de realizar 1.000.000 de iterações. Ao se paralelizar esse problema num computador com 4 processadores poderíamos diminuir o tempo computacional para algo em torno de 25% do tempo gasto pelo codigo sequencial. E ao se utilizar uma GPU? as GPUs contam com milhares de processadores, desta forma o tempo de computação pode ser reduzido à um tempo irrisório.
Existem no mercado uma enorme variedade de placas de vídeo e atualmente existem placas desenhadas especialmente para processamento em paralelo. Algumas delas (mais caras) possuem inclusive uma memória maior, permitindo ao usuário executar processos mais complexos e que exigem maior espaço para alocação.
Na ausência de uma placa de vídeo me atenho aos exemplos realizados por sortudos que à possuem. Neste site temos acesso à diversos exemplos aos quais o tempo computacional utilizando CPU e utilizando GPU são comparados: Computação em GPU.
Em resumo os exemplos mostram (no R, utilizando o pacote rpud) uma melhora impressionante no tempo de execução dos códigos. Apenas para reforçar a mensagem atente para o exemplo do cluster hierárquico. O tempo de execução utilizando a função paralelizada em GPU foi extremamente mais rápida se reduzindo a menos de cinco segundos enquanto a função original leva mais de um minuto (Caso de 4000 vetores).
Obviamente utilizar a programação em GPU é um bom negócio, portanto de posse de uma placa experimente melhorar a performance do seu código.
Referências
https://en.wikipedia.org/wiki/Parallel_computing
https://www.r-bloggers.com/how-to-go-parallel-in-r-basics-tips/
http://blog.aicry.com/r-parallel-computing-in-5-minutes/
https://computing.llnl.gov/tutorials/parallel_comp/
https://cran.r-project.org/web/packages/doParallel/vignettes/gettingstartedParallel.pdf
https://www.r-bloggers.com/the-wonders-of-foreach/
ftp://cran.r-project.org/pub/R/web/packages/foreach/vignettes/foreach.pdf
https://cran.r-project.org/web/packages/foreach/foreach.pdf
